文章内容
- 素性测试 (Primality test)
- 什么是质数?
- 遍历取模
- 遍历取模函数式版本
- 正则表达式法
- 开方优化
- 埃拉托斯特尼筛法:用质数找出质数
- 性能比较
最近在刷笔试题,有几个关于质数的题目,总结一下判断是否为质数的几个方法。
素性测试 (Primality test)
素性测试或素数判定,是检验一个给定的整数是否为素数的测试。 维基百科
什么是质数?
质数(Prime number,又称素数),指在大于1的自然数中,除了1和该数自身外,无法被其他自然数整除的数(也可定义为只有1与该数本身两个正因数的数)。
大于1的自然数若不是素数,则称之为合数(也称为合成数)。
遍历取模
判断当前整数是否为质数最常规的方法,就是让它与所有小于它的数(且大于1)取模。
取模运算是求两个数相除的余数。余数为0,说明能被整除。
只要能被其中一个数整除即为合数,不能被所有整除即为质数。
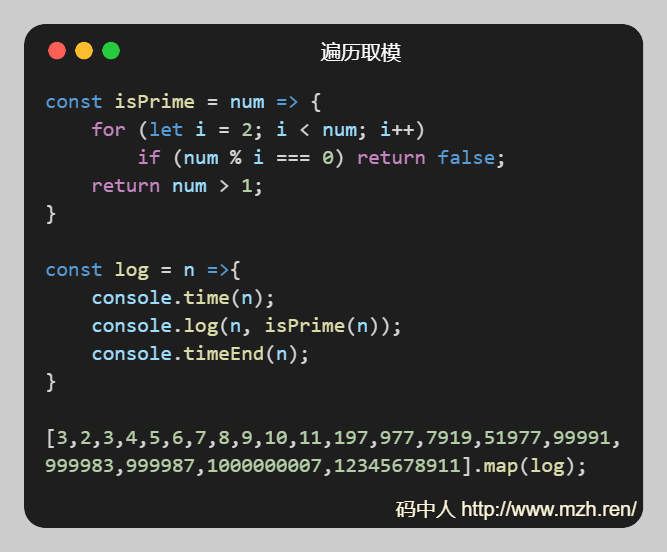
以上代码时间复杂度为:O(n),被检测的数越大,在经历的循环次数越多,耗时越大。
...
...
9: 0.030ms
10 false
10: 0.025ms
11 true
11: 0.025ms
197 true
197: 0.034ms
977 true
977: 0.063ms
7919 true
7919: 0.362ms
51977 true
51977: 2.624ms
99991 true
99991: 1.359ms
999983 true
999983: 5.989ms
999987 false
999987: 0.024ms
1000000007 true
1000000007: 6007.705ms
12345678911 false
12345678911: 0.046ms
如上,需要6秒钟才能判断1000000007是个质数。
遍历取模函数式版本
可以用数组方法替代for循环。

坏处就是需要生成一个1至n的数组,增加了空间复杂度。n越大,数组越大。
虽然JavaScript中数组长度的最大值为 2**32-1,但实际上肯定到不到2**32-1,如10000000000就不行了。可能跟电脑的配置有关。

因无法生成1000000007长度的数组,以上代码无法检测出1000000007等一系列大的质数。
正则表达式法

这个方法很酷,详细的解释,请戳:A wild way to check if a number is prime using a regular expression | by Mark Sauer-Utley | ITNEXT
https://itnext.io/a-wild-way-to-check-if-a-number-is-prime-using-a-regular-expression-4edfb725f895
简单解释:
^1?$|^(11+?)\1+$
这个正则表达式可以匹配所有不是质数的数(合数,以及0,1),模式如下图所示:
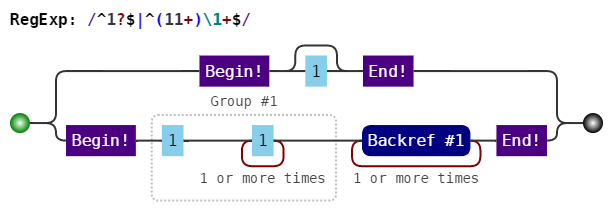
这个正则表达式主要是通过将数值转化为字符1的个数来实现监测质数的功能的。此正则表达式分成 由”|”分割两部分: /^1?$/和/^(11+?)\1+$/。
前一部分匹配0或1,这两个数不是质数。
后一部分(11+?)表示至少有两个1,(11+?)\1中的\1表示对前面的匹配的引用。\1+表示前面的(11+?)出现至少一次,相当于(11+?){2,}。整个式子的含义为至少出现两次(11+?)。也就是说,所匹配的数可以写成两个大于2的整数的乘积。而?通过backtrace穷举所有的可能行,从而完成匹配所有的合数。
因此,两部分使用|连接,不匹配的就只能是质数了。
存在问题:
需要生成 “1”.repeat(n) 的字符串,n越大,字符串越大,空间复杂度越大。
同样,理论上js字符串的长度为2**53-1,实际上1000000000就不行了。
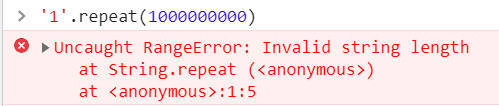
100000000可以,但其内存占用100mb以上。

所以正则表达式方法也检测不了大的质数。
开方优化
以上方案中,遍历取模是适用而比较广的,它能检测到质数相对较大。
只要想办法减少遍历次数,即可提升性能。
因为一个数的最小质因数一定会小于或等于这个数的开方(平方根)。
质因数(素因数或质因子)在数论里是指能整除给定正整数的质数。除了1以外,两个没有其他共同质因子的正整数称为互质。
1没有质因子。
5只有1个质因子,5本身。(5是质数)
6的质因子是2和3。(6 = 2 × 3)
2、4、8、16等只有1个质因子:2。(2是质数,4 =2²,8 = 2³,如此类推)
10有2个质因子:2和5。(10 = 2 × 5)
如100的开方是10,其质因数 2和5都小于10。121的质因数11,等于其开方11。
因为一个数的最小质因数小于或等于其开方,所以只需要遍历到其开方数就可以了。

其性能大大提升。
筛法:用质数查找质数
开方优化方法将循环次数从n减少到Math.sqrt(n),性能大幅度提升。
那么能否进一步减少循环次数?答案是肯定的。
遍历取模是对质数才有效,在有限的整数序列中,质数远少于合数。如果只对质数集合遍历,将大大循环次数。
所以,关键在于找出小于Math.sqrt(n)的质数集合。
此时需用筛法:筛法(挨拉托色尼筛法)是一种用来求所有小于N的素数的方法。把从2(素数是指大于1的自然数)开始的某一范围内的正整数从小到大按顺序排列,逐步筛掉非素数留下素数。
筛法求素数的基本思想是:把从2到N的一组正整数从小到大按顺序排列。从中依次删除2的倍数、3的倍数、5的倍数,直到根号N的倍数为止,剩余的即为2~N之间的所有素数。
所以,100以内的素数都可以通过2,3,5,7筛选出来:

代码实现即为:

我们需要一个[2,3,5,7… Math.sqrt(n)]集合,可以通过生成器实现:

genPrimes将生成一个质数有序集合,判定质数只需对该集合遍历取模就行。

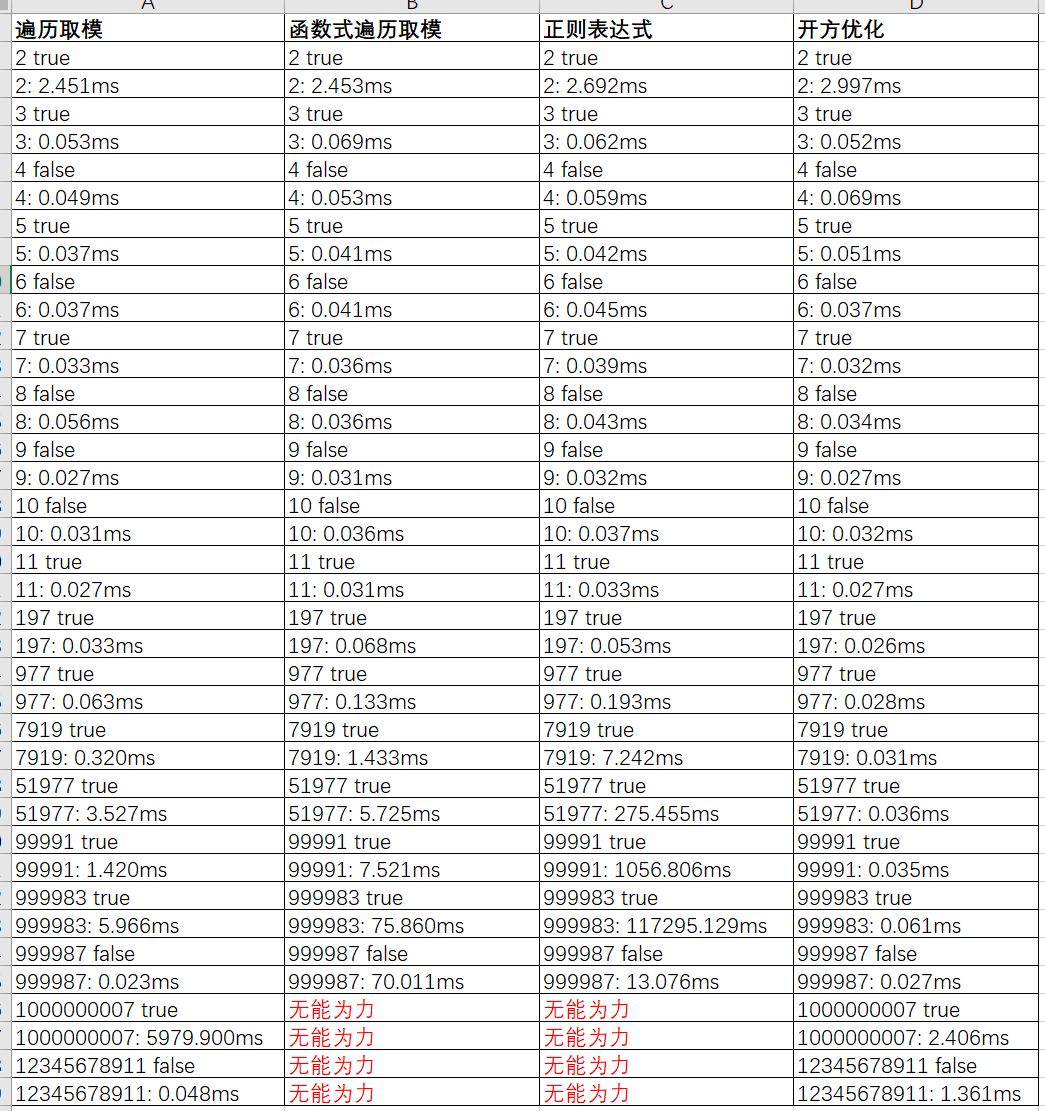
性能比较
筛法 ≈> 开方优化
筛法法因维护ALL_PRIMES集合,必然增加算法空间复杂度。所以在数值较小时,筛法与简单开方优化差不多。
但数值越大,筛法时间效率越高。
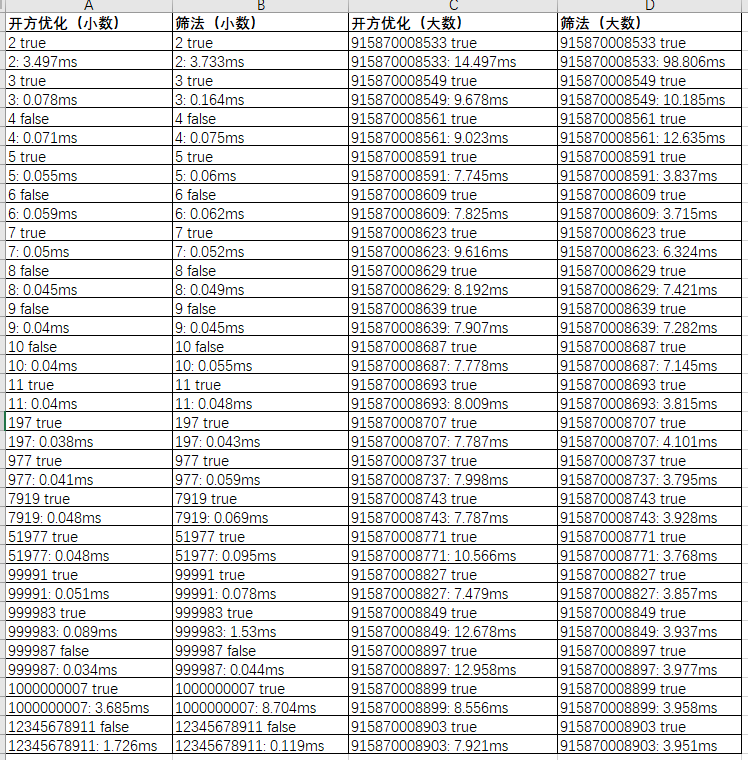
开方优化»遍历取模>函数式遍历取模>正则表达式。
你还知道哪些质数判定的方法,请留言告诉我!
